真空管アンプの工作、原理、設計まで
電気知識から真空管の原理、アンプの原理まで
最近のプロジェクト紹介、質問掲示板などの真空管ギターアンプ製作センターを始めました
アンプやペダルを販売しています

本サイトが書籍になりました

アンプの周波数特性について
ここまでで見てきたように、増幅回路にはコンデンサがいくつか入っている。コンデンサは高い周波数を通し、低い周波数を阻止するので、これによっておのずと増幅回路の周波数特性が決まってくる。これは予想できると思うが、周波数特性というのは音の質にもっともダイレクトに影響する。こもった音は高域が出ていないせいだし、キンキンした音は低域が出ていないせい、というわけだ。
オーディオ用のアンプでは、普通、周波数特性はフラットであるほど良い、とされている。人間の可聴帯域はおよそ20Hzから20kHzだが、少なくともこの帯域では増幅度が落ちたり、ピークを作ったりすること無く平坦であることが要求されるわけだ。一方、ギターアンプでは事情はかなり異なる。
一般にギターアンプは周波数特性をフラットにはせず、独特な周波数特性を持たせて、エレキギターで弾いたときに「カッコいい音」になるように調整されている。エレキギター自体の音域もそれほど広くはなく80Hzから5kHzぐらいであり、余計な低域や余計な高域は、エレキギターのもっとも「おいしい音域」を阻害しないように、削ったりするのが普通である。また、ご存知の通りたいていのギターアンプにはトーンコントロール回路が付いていて、周波数特性自体をツマミで好きにグリグリ変えて使うのが普通である。
さらにギターアンプでは、増幅回路をほとんど何らか歪ませて使うことが多い。つまり、ギターの信号が何段もの増幅回路を通ってスピーカーに到達するとき、いくつかの段の増幅回路では信号が過大入力になって歪んでいる、ということがギターアンプの一般的な使い方では起こっているわけだ。エレキギター弾きならたいていの人が、アンプが「どれぐらいカッコよく歪むか」にこだわっていると思う。そして、この歪みに周波数特性が複雑に絡み合っているのである。
たとえば、ギター信号を「高域を落としてから歪ませる」のと「歪ませてから高域を落とす」のでは、出てくる音がまるで異なる。どっちがいい音かは、私は知らない、それはギターアンプの「個性」なのである。自分はマーシャル使いではないが、たまにマーシャルで弾くと「マーシャルってのは高音がギスギスしてるくせに何でああ低音弦に腰がある太い音がするのだ!」と感心することがあるが、この辺のトーンキャラクターの秘密は、アンプ回路のどこで、どれだけ周波数特性をいじって、そしてどこでそれを歪ませるか、という組み合わせにあることが多いようである。回路を見ると、変哲なくコンデンサーが入っているだけだが、そこには多大なノウハウが込められているのである。
周波数特性がどうなっているかを回路図から調べようとしたとき、では、これらコンデンサの値つまり0.022μFとかなんとかだけを見れば分かるのか、というとそうではない。コンデンサは「抵抗」と組み合わされて周波数特性を形作るので、コンデンサCと抵抗Rはペアで考えないといけない。さて、というわけで、本章では、このCRによる周波数の変化の原理について解説しよう。
CRによる周波数特性の変化とデシベル
まず、コンデンサと抵抗が形作る周波数特性の一般的な話しからしよう。原理編のところで、コンデンサは直流は通さず、周波数が高いほどよく通す、という性質について説明した。例えば、増幅回路のRC結合回路のようにコンデンサが回路に直列に入ると、周波数が低い信号ほど通りにくくなるので低域が落ちる。それでは、具体的にどれぐらい落ちるのだろうか。
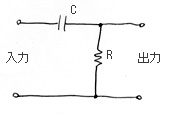
下の左の図のような単純な基本回路を考える。このとき、入出力の周波数特性は右の図のようになり、低域が落ちる形になる。このように、信号を選択的に通したり、阻止したりする回路をフィルタと言う。ここでの回路は、低域を通しにくいのでローカットフィルタと言いわれる。あるいは、高域を通す、という意味でハイパスフィルタ(HPFと略されたりする)とも言われる。
 |
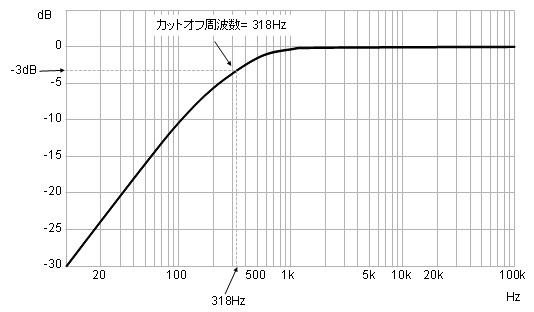 |
| CRによるローカットフィルタの基本回路 | ローカットフィルタの周波数特性(C=0.01μF、R=50kΩのとき) |
A = 20 log10 a …(1式)例えば2倍の場合は、20 log10 2 ≒ 6dB、0.5倍は20 log10 0.5 ≒ -6dBである。このように、増幅では値がプラスに、減衰ではマイナスになる。また、多段増幅回路などで、例えば100倍の回路を2段つなぐと、掛け算して100×100=10000倍の増幅器になるが、デシベルではこれが足し算になる。100倍は40dB (= 20 log10 100)なので、2段つなげると40+40=80dBの増幅回路になる。周波数特性でよく出てくるのが-3dBで、比率では約0.7である。また、-1dBは約0.9である。図の周波数特性はこのdBを使って描いた特性になっている。ここで、-3dB(つまり信号が0.7倍に落ちたポイント)の周波数をカットオフ周波数といい、次の式で計算できる。
1
f = ---------- …(2式)
2 π C R
例えば、C=0.01μF、R=50kΩのときは
1
f = ---------------------------------- = 318 Hz …(3式)
2 ・ 3.14 ・ 0.01x 10-6 ・ 50 x 103
となり、318Hzのときに-3dB減衰する。上図の特性は、このときのものである。
 |
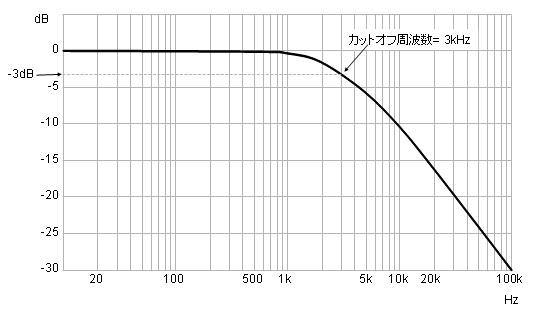 |
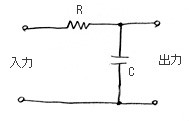
| CRによるハイカットフィルタの基本回路 | ローカットフィルタの周波数特性(C=0.01μF、R=5.3kΩのとき) |
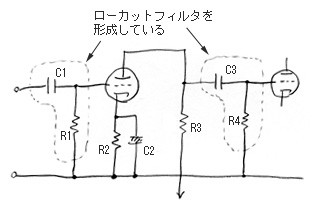 |
| 結合コンデンサによるローカットフィルタ形成 |
1
f = ------------ …(4式)
2 π C3 R4
で計算できる。ここで厳密には、前段の負荷抵抗R3と真空管の内部抵抗rpが並列になった抵抗が上記R4部分に加算されるのだが、R4はこれらよりかなり大きいのがふつうなので近似的に上式でだいじょうぶである。
1 1
C = ---------- = ---------------------- = 0.017 μF …(5式)
2 π f R4 2×3.14×20×470×103
これで、0.017μFより大きい値のコンデンサを使えばよいことが分かる。実際には、現代のオーディオアンプでは、20Hzで-3dBは少し不足で、-1dB以下なのがふつうである。この場合、カットオフ周波数を半分の10Hzにして計算すれば約-1dBになる。このときCの値は倍になり0.034μFである。
1 1
f = ---------- = ------------------------------ = 7.2 Hz …(6式)
2 π C R 2×3.14×0.022×10-6×1×106
・次の0.022μFでは、220kΩの抵抗(グリッドリーク抵抗)が入っているので
1 1
f = ---------- = -------------------------------- = 33 Hz …(7式)
2 π C R 2×3.14×0.022×10-6×220×103
低い周波数はそこそこにカットした形になっていて、確かに、オーディオアンプの場合とは異なっている。
次はカソードのバイパスコンデンサC2である。このバイパスコンデンサは片側がグランドに落ちていて、一見前に出てきたハイカットフィルタのパターンに見えるが、これは違う。これは電圧増幅回路の原理で説明した、カソード抵抗の電流帰還による増幅率低下を防ぐためのもので、コンデンサによって低域が落ちる形の特性になる。そのため、周波数をフラットにするためには、このC2は十分大きくする。たいがい、ここは22μFから220μFぐらいでエイヤと決められていることが多い。
計算でカットオフを出すこともできるが、真空管のμやrpなども関係して複雑なので他書に譲るとして、計算例だけ示しておこう。たとえば、以前出てきた12AX7の電圧増幅回路においては、カソード抵抗が2.8kΩで、バイパスコンデンサに100μFを使うと、カットオフ周波数は0.6Hzぐらいになる。十分に低い値に設定されている。
5極管の場合のスクリーングリッドに入るコンデンサだが、これも計算は複雑である。このコンデンサも低域が落ちる形になる。だいたい、スクリーングリッド抵抗の値を使って、結合コンデンサの計算と同じ(1)式でめどはつけられるはずだ。このスクリーングリッドのバイパスコンデンサには1μF以上の電解コンデンサを使うことが多く、たとえば10μFもあれば低域はかなり延び、オーディオとしても問題ない。もちろん、スクリーングリッド抵抗が300kΩなどと、グリッドリーク抵抗並みに大きければ、結合コンデンサと同じような感覚で、電解コンデンサを使わず0.47μFぐらいが入っているときもある。
以上、結合コンデンサとカソードバイパスコンデンサとスクリーングリッドのバイパスコンデンサについて述べた。すべて低域を落とす働きになるが、バイパスコンデンサ系は増幅回路の出力内部抵抗と係わったり、歪みと係わったりするため、その振る舞いはかなり複雑である。オーディオアンプでは、これらのコンデンサは、「ま、でかくしとけばいいや」で済んでしまったりすることが多いが、ギターアンプでは、このへんのコンデンサの値の調整は、かなり「遊び甲斐」があると言えよう。
それから、オーディオ用途だと、以上のコンデンサは大きければ大きいほどいいようにも見えるが、あまり大きくすると、大きさや値段もはるだけでなく、弊害が現れる場合があり、定石の回路で使われている値が妥当と考えておいた方がいい。たとえば、ときどき、低域特性を「超良くしよう」としてカソードバイパスコンデンサに10000μFを使ってみた、などという人がネットに現れたりするが、いくら6.3V、10000μFの電解コンデンサが安値で売っていたとしても、これはヤバイ。電源スイッチを入れたとき、10000μFぐらいだと充電されるまでしばらくの間、両端の電圧はゼロボルトからなかなか動かず、その間、プレートに過大電流が流れてしまったりする。
それから、故意にコンデンサを小さめにして音のバランスを取ったり、超低域の発振を抑えたり、NFBの発振を抑えたり、という使い方もされるが、この辺になるとかなり上級である。
高域落ち(ハイ落ち)について
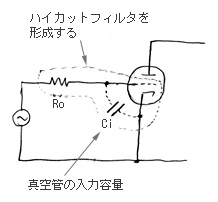 |
真空管の入力容量によるハイ落ち |
これまでは低域落ちの話しばかりだったが、高域落ち(ハイ落ちという)も起こる。以前の図のCRによるハイカットフィルタ回路のように信号に対してコンデンサが並列にグランドに落ちるように入るとハイ落ちが起こるが、オーディオ用の増幅回路にはふつうこの手のコンデンサは明示的には現れず、見えないコンデンサとして存在する。この見えないコンデンサで一番大きいのが、真空管の入力容量とシールド線の容量である。
真空管の入力容量については、詳しくは他書に譲るが、5極管の場合、数pFでほとんど問題にならないが、3極管では数十から数百pFになることがあり要注意である。これまでに出てきた回路のようなカソード接地の場合、入力容量は真空管の増幅率が大きいほど大きくなり、12AX7で約100pF、12AU7で約20pF、2A3で約60pFぐらいの値である(ミラー効果と呼ばれる現象により、増幅率が大きいほど見かけの入力容量が増加する)。
この場合、この真空管を駆動する前段の内部抵抗Roと、図のようにハイカットフィルタを形成するので、ハイが落ちる。
例として、図のように12AX7の2段増幅で、1段目の12AX7をカソードバイパスコンデンサを抜きにして使ったとする。
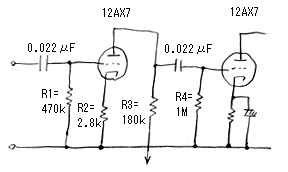 |
| 12AX7の2段増幅回路でのハイ落ち |
rp' = rp + R2 ・ ( μ + 1 ) = 80 + 2.8 ・ ( 100 + 1 ) = 363kΩ …(8式)前段側の内部抵抗Roは、rp'と負荷抵抗R3、次の段のグリッドリーク抵抗R4の3つを並列にした値になる。
1 1
Ro = ------------------------ = ----------------------- = 107kΩ …(9式)
1 1 1 1 1 1
---- + --- + ---- ---- + --- + ----
rp' R3 R4 363 180 1000
これで、12AX7の入力容量Ciは100pFなので、カットオフ周波数fcは次のように計算できる。
1 1
fc = ---------- = -------------------------- = 14.9kHz …(10式)
2 π Ci Ro 2 π 100×10-12 ・ 96×103
このように14.9kHzで-3dB落ちてしまうことが分かる。入力容量の高い3極管を、内部抵抗の高い球で、さらにカソードバイパスコンデンサ無しで駆動するときは要注意なわけだ。
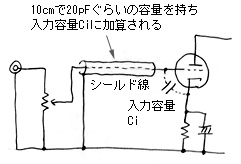 |
グリッドへの配線にシールド線を使ったときのハイ落ち |
また、内部配線で使うシールド線だが、これもけっこう大きな容量を持っている。ふつうのシールド線で10cmで20pFていどあるので、30cmも引き回せば60pFになって、これを右の図のように真空管のグリッドへの配線に使ってしまうと、真空管の入力容量にプラスされるので事態はさらに悪化する。
このように、見えないところに特性劣化は隠れている。20kHz以上でもずっとハイが伸びているような現代型オーディオのハイグレードアンプを目指すときは、これらに注意して設計しないといけないわけだ。ところで、ギターアンプの場合は、例によってこの限りではなく、わざとハイを落とすために、いろんなところでコンデンサがパラに入っていたりするのを見かける。それからギターアンプに定番のトーンコントロール回路については、また項を改めて解説する。
ちなみに、エレキギターのケーブルをシールドと称するが、あれもその名の通りシールド線で、同じような容量を持っている。仮にそのへんのシールド線と同じく20pF/10cmだとして、ロックパンク系の人のように20mぐらいのシールドで客席へ降りて弾くなんてことをやっているとすると、20mのシールドの容量はなんと4000pFになる。このコンデンサ成分は、エレキギターのギターマイクの内部抵抗とハイカットフィルタを形成してハイ落ちになる。今、仮に、エレキギター側のインピーダンスを50kΩだとしよう(実際にはギターマイクのインピーダンスは周波数により変化し、さらにギター側トーンコントロール回路なども入るので一概には決まらない)。この4000pFと50kΩで形成されるハイカットフィルタのカットオフ周波数を計算すると
1 1
f = ---------- = ------------------------------ = 800Hz …(11式)
2 π C R 2 π 4000×10-12 × 50 ×103
なんと800Hzである。800Hzと言えばA=440Hzのオクターブ上ぐらいなので、もう、1弦、2弦の音は思い切り減衰域に入ってしまう。これではハイ落ちまくりのモコモコの音になるに決まっている。まあ、こういうときのためにもギターアンプにはトーンコントール回路ってのが付いてるわけで、「なんだ、モコモコだな、ま、トレブル10、ついでにベースはゼロでディストーション全開だ!」と、まあ、このようになり、骨太のパンクロッカーは20メートルのシールドに精神的に打ち勝つので別にいいのだが、この事情は押さえておいた方がよい。
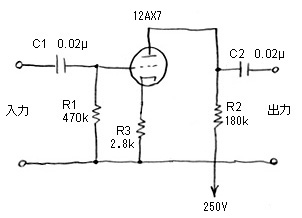 |
カソードのバイパスコンデンサが無い回路 |
rp' = rp + R3 ・ ( μ + 1 ) …(12式)
ここでμというのもデータシートに書かれている電圧増幅率という定数で、12AX7であればμ=100である。ここで、上の図のようにカソードのバイパスコンデンサが無いときのrp'は、カソード抵抗が2.8kΩなので、
rp' = 80 + 2.8 ・ ( 100 + 1 ) = 363kΩ …(13式)となり、バイパスコンデンサのあるときが80kΩで、無いときがこのように363kΩになり、内部抵抗はかなり大きくなることが分かる。このときの増幅回路のゲインAは、設計編のここの(5)式で計算できるのだが、見かけで大きくなった内部抵抗rp'で次のように計算される。
RL 130
A = μ ------------ = 100 ----------- = 26 …(14式)
rp' + RL 363 + 130
ちなみに、バイパスコンデンサが入っているときはrp=80kΩがそのまま入り、次の通りである。
RL 130
A = μ ----------- = 100 ---------- = 62 …(15式)
rp + RL 80 + 130
このように、バイパスコンデンサが入っていたときは62だが、このコンデンサが無いとこれが26に落ちていることが分かる。この性質を利用して、回路のゲインがありすぎて困る場合など、わざとバイパスコンデンサを外してゲインを落とすことがある。ただ、内部抵抗は増加するので、前の項で説明したように、次段の真空管のグリッドの入力容量と共にハイカットフィルタを形成し、高域の応答が落ちることがあり、要注意である。
■小さいカソードバイパスコンデンサが入ったときの周波数特性
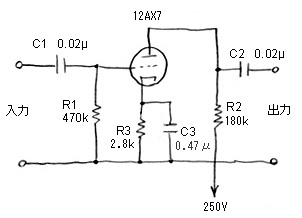 |
カソードのバイパスコンデンサが小さいとき |
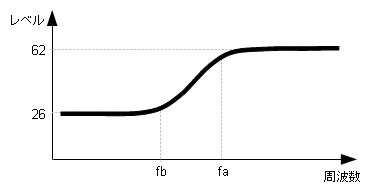 |
| カソードのバイパスコンデンサが小さいときの周波数特性 |
480
fa(Hz) = -------------------- …(16式)
C3(μF) × R3(kΩ)
53
fb(Hz) = -------------------- …(17式)
C3(μF) × R3(kΩ)
この式で右上の図の回路についてちょっと計算してみよう。C3とR3のところにはそれぞれμFとkΩを入れることに注意である。C3が0.47μでR3が3kなので
480
fa = ----------- = 340 (Hz) …(18式)
0.47 × 3
となり340Hzあたりから落ちてくる。同じように(17)式でfbを計算すると38Hzになる。このように、300Hzあたりより低い周波数をそこそこにカットした特性になることが分かる。
ちなみに、よくオーディオアンプなどではこのカソードバイパスコンデンサにほとんど慣習のように100μFを使ったりするが、カソード抵抗をたとえば1kΩとしてfaを(16)式で計算してみると4.8Hzになる。20Hzより十分低い値になっていることが分かる。
繰り返すが、これらの式は目安にしかならない。ここで上級の方のために前掲の(16)式と(17)式をどのように導いたか書いておこう。非常に単純で、コンデンサC3のインピーダンスがカソード抵抗R3の1/3のときにfa、3倍のときにfbとした式である。これは自分で実際にいろいろやってみて、まあまあ、これで使えないこともないかな、と判断して載せている。
ちなみに、本当の計算式はjωという複素数の絶対値計算などが入った面倒な式になる。こちらもマニアックな方のためにココに数式だけ載せておく。もっともさいきんはそんな大時代的な数式など使わず、SPICEなどの回路シミュレーションソフトを使って周波数特性を計算するのが一般であろう。
さて、この中途半端なカソードバイパスコンデンサに何の意味があるのかというと、実はギターアンプではここに小さなコンデンサを使って低域を意図的に削るようなことをしたりするのである。フェンダーのアンプなどではほとんど見かけないが、近代的なメタル系のハイゲインアンプと呼ばれる過激に歪むアンプなどでは、けっこうこのコンデンサで低域をコントロールするテクニックが使われている。たとえば、かのSoldanoのアンプのドライバー段では12AX7のカソード抵抗1.8kに1μFという小さなバイパスコンデンサをつけている。これを上の式で計算すると落ちはじめの目安は270Hzになり、この辺に音の秘密が隠れていそうな雰囲気がある。