真空管の話にいきなり入る前に、まずは、基本の基本に属する「電気」について簡単に説明しておこう。ここでは、なるべく直感的に「わかる」ように、教科書的な厳密さは抜きにして解説してみる。これを読んで興味を持った人は、ぜひ、もっと専門的な本で勉強してみて頂きたい。
電気とは
 |
 |
| 電圧と電流 |
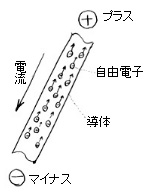
電流と自由電子 |
例えば、図のように電池のプラスとマイナスの両端に豆電球をつなげば、プラスからマイナスに向かって電流が流れて電球が光る。電池の両端に出ているのが
電圧
、導線と電球に流れているのが
電流
で、それぞれ単位は
ボルト(V)
と
アンペア(A)
である。電圧が大きければ、電流もたくさん流れ、結果、電球が明るくなる、というのは感覚的になるほどであろう。では、電流の流れている導線と電球の中で、何が起こっているかというと、この中では、図のようにマイナスの電気を持った「電子」という極小の粒が流れている。ここでの電子は、自由電子といって、導体(電気を通す物体)の中で自由に動き回れる電子である。導体の両端に電圧をかけることで、この自由電子のマイナスがプラスと引き合って、マイナス側からプラス側へ移動して行くのだ。このように、電子が動いている方向と、電流が流れる方向は逆になっている。歴史的な経緯によって、逆になってしまったらしい。ちなみに、電気の伝わる速度は光速と同じだが、電子自体が光速で導体の中を移動しているのではない。電子の平均移動速度は意外と遅く、普通はカメが歩くよりのろい。なのになぜ光速で電気が伝わるかというと、導体の両端に電圧をかけたとたん、中の電子が一斉に動き出すからである。まあ、トコロテンの片側を押すと、瞬時に逆側から押し出されるのを連想してもいいかもしれない(ちょっと違うが。あ、あと、たとえが古いが 笑)。
電気抵抗
電流というのは、1秒間に、どれだけの数の電子が通過するかでその大きさが定義されている。たくさん電子が通過すれば電流値が大きいというわけである。さて、ここで
電気抵抗
というのは、この電子の通りにくさを表している。
抵抗
という素子は、中に不純物が入っていて、電子が動きにくくなっていて、それで電流の通りを妨げるのである。そうすると、移動する電子の量も少なくなり、流れる電流の値が小さくなる。抵抗値が大きくなると電流は減る、というわけだ。この電気抵抗の単位が
オーム
で、略号は
Ω
である。
オームの法則
 |
オームの法則
|
 |
| オームの法則の別解釈 |
これまでの説明で、電圧が大きくなればたくさん電流が流れ、抵抗が大きくなれば電流は減る、という関係が出てきた。実は、この抵抗R(Ω)と電流I(A)、そして電圧E(V)の関係は単純な比例関係になっていて、これが次の有名な
オームの法則
である。
E
I = --- …(1式)
R
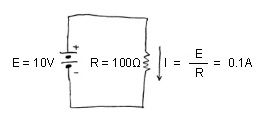
たとえば右上の図のように、10Vの電池に100Ωの抵抗をつなぐと、流れる電流は10/100=0.1Aである。この式を別の書き方にすると、次のようになる。
E = R I …(2式)
E
R = --- …(3式)
I
この3つの式は全部同じ式だが、何は無くともこれだけは覚えておくとよい。極端な話し、真空管アンプの設計は、このオームの法則と、次に出てくるワット数の計算式だけあれば、なんとか出来てしまったりするのだ。学校教育的に言うと、数学は必要なく、加減乗除の算数と、あと作図ができれば真空管アンプは何とかなる。
さて、ここまでの説明では、抵抗の両端に電圧をかけるとE/Rという大きさの電流が流れる、というものだった。これは言い方だけを変えると、図のように、「抵抗Rに電流Iを流すと、電流の向きと逆の電圧RIを発生する」と考えることもできる。この考え方はわりといろんな局面で出てくるので、ニュアンスを覚えておこう。
ところで、この後に交流の話しが出てくるが、このオームの法則は交流でも直流でも同じく使える。
電力
|
| 抵抗と消費電力 |
電力というのは、電気が1秒間あたりにする
仕事
の量を表す。詳しくしゃべり出すと物理の授業になってしまうので省略するが、ここでいう
仕事
というのはふつうエネルギーと言っているものである。平たく言えば電力とは、電気を使って、明かりをつけたり、電熱器を熱したり、モーターを回したり、ギターアンプを爆音で鳴らしたりするときに消費されるエネルギーの量である。
電力の単位は
ワット
(略号はW)である。この電力P(W)は、電圧E(V)と電流I(A)の単純な掛け算で計算できる、すなわち
P = E I …(4式)
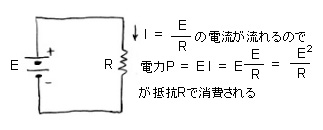
である。たとえば、図のように、抵抗Rの両端にEの電圧がかかると、オームの法則から、流れる電流はE/Rだ。したがって、抵抗で消費される電力Pは、この電流E/Rに電圧Eを掛け算して
E2
P = --- …(5式)
R
と計算できる。あるいは、抵抗にかかる電圧Eはオームの法則よりRIになるので、(4)式にこれを代入して、次の式でも電力を計算できる。
P = I2 R …(6式)
電力というのはエネルギーなので、このエネルギーは、熱になったり、光になったり、動力になったりして、要は外に対して仕事をする。単純な抵抗素子に電圧をかけて電力を発生させると、抵抗の場合はそのすべてが熱に変わる。つまりは抵抗が熱くなるということだ。ひとつの抵抗で消費される電力は上記の式で簡単に計算できる。例えば、1kΩの抵抗の両端に10Vの電圧がかかっている場合
E2 10 × 10
P = --- = ---------- = 0.1 W …(7式)
R 1000
となり、0.1Wと計算できる。前に、抵抗には指定ワット数がある、と説明した。これは、この電力によって発生する熱で抵抗の温度が上昇して、その温度上昇に耐えられるだけのワット数を表したものである。当然ながら、図体の大きい素子ほど同じ熱量でも温度上昇が少ないので大きな電力に耐えられる。上記0.1Wであれば、およそ1/8W(0.125W)だが、抵抗の使用には余裕を持たなければならず、ふつう3倍ぐらいのワット数のものを使う。この場合、3倍で0.3Wになるので、1/4W(0.25W)でもまあいいが、ちょっと足りないので1/2W(0.5W)のタイプを使うのが無難、という感じになる。
抵抗では電力は熱になるが、スピーカーではコーン紙を動かす動力に変換されて、これが音になる。スピーカーで消費される電力が大きいほど、でかい音がするわけだ。これがアンプの出力で言うところのワット数である。
抵抗の合成
|
| 抵抗の合成 |
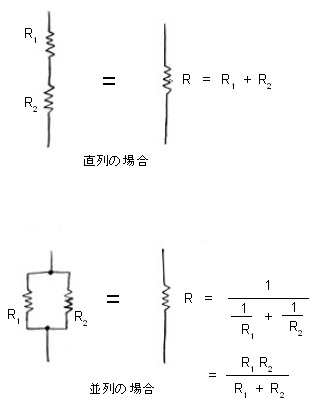
抵抗は、直列につないだり、並列につないだりすることで合成することができる。図の上のように、抵抗R
1と抵抗R
2を直列につなぐと、その合成抵抗Rは
R = R1 + R2 …(8式)
になる。一方、図の下のように並列につなぐと
R1 R2
R = -------- …(9式)
R1 + R2
になる。この2つの式は実はオームの法則を知っていれば簡単に導き出すことができるのだが、ここでは省略する。では、例をあげてみよう。2kΩと3kΩの抵抗を直列にすると
2 + 3 = 5kΩ …(10式)
となり、5kΩの抵抗になる。これが並列だと
2 × 3
-------- = 1.2kΩ …(11式)
2 + 3
で、1.2kΩの抵抗になる。直列にすると、必ず元の2つの抵抗より大きくなり、逆に並列にすると必ず小さくなる。この性質を使って、手持ちの限られた抵抗で、手持ちにない抵抗の値を作り出すことができる。
では抵抗のワット数はどうだろう。同じ値の抵抗2本なら、直列にした場合も並列にした場合も、ワット数は単純な足し算になる。1kΩ1Wの抵抗を直列にすれば2kΩ2Wに、並列にすれば500Ω2Wになる。しかし、2つの抵抗の値が変わるとワット数は単純な足し算にはならない。各抵抗の値とその両端の電圧(または流れる電流)から各々計算して求めるのだが、ややこしいので詳しくは省略する。そんなわけで、抵抗を合成して使うときは、合成した抵抗のワット数は増えないと考えておいた方が無難だ(それでも、完全に安全とはいえない)。自分は、というと、実験のときには合成抵抗はよく使うが、本番のときにはほとんど使わない。
直流と交流
|
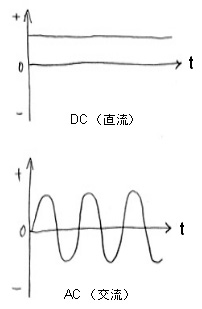
| 直流と交流 |
直流は、プラスとマイナスが変わらない一方向の電気である。それに対して交流はプラスとマイナスが周期的に逆になるような電気をいう。乾電池の電気は直流、家庭のコンセントから出てくるのが交流だ。直流は
DC(Direct Current) 、交流は
AC (Altanative Current)と表記する。図のようにACの代表的なのはサインカーブをしており、1秒に何回向きが逆になるかによって周波数というものがある。単位は
Hz
(ヘルツ)で、1秒間の反転の回数になる。家庭の電気は、関東では50Hz、関西では60Hzである。知ってのように音の信号も交流で、人間の耳に聞こえる周波数はおよそ20Hz〜20kHzである。
DCの電圧(あるいは電流)の表記には一種類しかないが、ACにおける電圧(以下、電圧で説明する)の表し方には何種類かある。ACの電圧は、ふつう
実効値
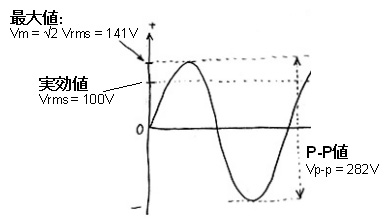
と呼ばれる量で表されている。日本の家庭のACは100Vだが、下図の左のように、これはサインカーブの一番大きいところ(ピーク)が100Vなのではない。このピークの値を
最大値
と呼ぶが、実効値Vrmsと最大値Vmには次の関係がある。
Vm = √2 Vrms ≒ 1.41 Vrms …(12式)
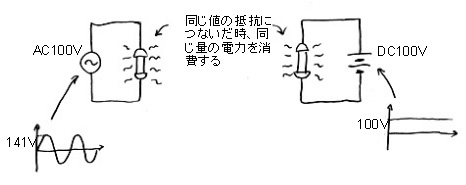
すなわち、実効値にルート2 (= √2 =1.41421356...)を掛け算すると最大値になる。なので、家庭のACの最大値は実は141Vあるのである。この実効値というのは、下図の右のように、同じ値の抵抗をACとDCにつないだときに、同じだけの電力を消費するときのDCの値なのだ。また、プラスのピークの値とマイナスのピークの値との差を使うことも時々あり、これを
ピーク・ツー・ピーク値
(P-P値)という。AC100VでのP-P値は282Vである。
|
|
| AC100Vの実効値、最大値、P-P値 |
交流の実効値の意味 |
コンデンサ
コンデンサは、
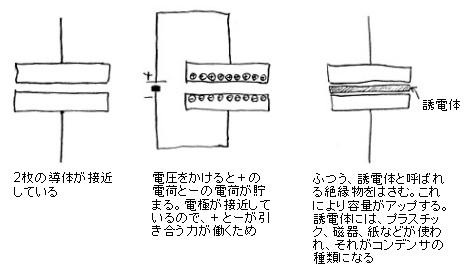
交流を通して直流を通さない素子
である。その構造は、下の図のようになっていて、ふたつの電極が接近して対面しているだけである。こんな風に離れていれば直流は永久に通しそうもないのはすぐ納得できるだろう。そこで、この2つの対面電極に電圧をかけると、プラスをかけた電極にはプラスの電荷が、そして、マイナスをかけた電極にはマイナスの電荷が貯まる。両者が接近していて、引き合う力が働くからである。ここで、貯まる電荷の量が多いほど、大きな容量のコンデンサということになる。結局、電気を貯める性質がある素子とも言えるわけで、そんなことからコンデンサは日本語では
蓄電器
と呼ばれる。ちなみに英語ではコンデンサとは言わずCapacitor(キャパシタ)と呼ぶ。
|
| コンデンサの構造 |
|
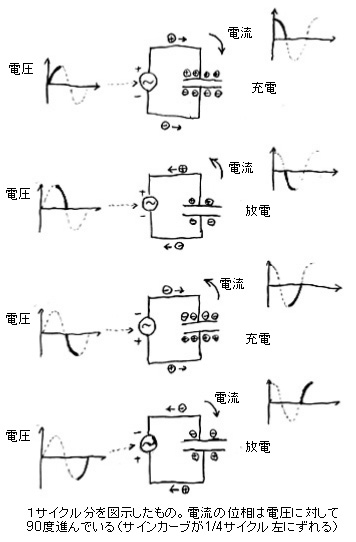
| コンデンサに交流が流れる様子 |
さてそれでは、なぜこれで交流を通してしまうのだろう? 交流の場合、図のように、あるときの電圧の方向で充電され、次のサイクルで電圧のプラスマイナスが逆になると、電極に貯まった電荷が信号源に向かって流れ、そして今度は逆方向に充電する、ということを繰り返す。そうすると、結果的に、交流の電流が常に流れていることになり、交流はコンデンサを通過する、ということになるのである。それから、図をよくよく見ると分かるのだが、入力の電圧変化と流れる電流の変化に1/4サイクル(90度位相とも言う)のずれが発生する。それはともかく、増幅回路では、この「直流は通さず交流は通す」という性質を利用して、様々なところに使われる。
コンデンサは直流をまったく通さないが、交流に対しては一種の抵抗として働く。一般に、交流に対する抵抗値を
インピーダンス
と呼び、以後もこの言葉を使おう。コンデンサでは、直流に近い低い周波数ほどインピーダンスが大きく、逆に高い周波数ではインピーダンスが小さくなる。コンデンサの値をC(F)とすると、インピーダンスZ(Ω)は、交流の周波数をf(Hz)とすると次の式で計算できる。
1
Z = ------- …(13式)
2πfC
例えば、0.01μFのコンデンサーは1kHzの交流に対しては
1
Z = ----------------------------- ≒ 16kΩ …(14式)
2π × 1000 × 0.01 × 10-6
という値になる。これが10kHzだったら1/10の1.6 kΩである。
コンデンサも抵抗と同じように合成できる。その値は抵抗のときとちょうど逆になる。C
1とC
2のコンデンサーを直列にすると合成容量Cは
C1 C2
C = --------- …(15式)
C1 + C2
になり、並列にすると
C = C1 + C2 …(16式)
になる。耐圧は、並列のときは2つのコンデンサの耐圧の低いほうの値になる。直列のときは、容量が同じなら一見倍になりそうな気もするが、実際には一概に言えず、低いほうの耐圧だと思ったほうが安全である。
コイル
|
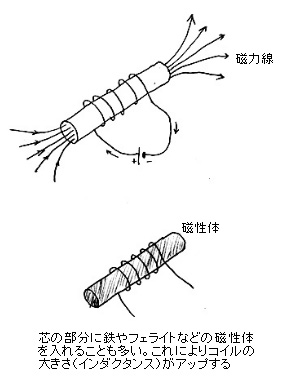
| コイルの構造 |
コイルは、ちょうどコンデンサと対になる素子で、その性質もちょうど逆で、
直流は通して交流は通しにくい素子である
。その構造は、その名のとおり導線をくるくる巻いたコイル状のものである。形はどうであれ、しょせんは導線なので直流はスカスカに通してしまう。では、なぜ交流を通しにくいのだろうか? コイルに電流が流れると、図のように、芯に当たる部分に磁力線というものが発生する。この磁力線には、いったん発生すると、その大きさを維持する、という性質があり、変化に対して抵抗するのだ。電流の大きさと向きが常に変化する交流の場合、その変化を打ち消そうとして、導線に逆側の電圧が発生し(逆起電力という)、電流の流れを妨げるのである。というわけで交流は通りにくくなる。変化のスピードが激しいほど、すなわち周波数が高いほど、この傾向は強くなる。
コイルは、直流に対する抵抗はゼロ(実際は導線の電気抵抗があるのでゼロではなく小さな値)だが、交流に対しては、コンデンサと同じように抵抗として働く。これもコンデンサのときとは逆に、周波数が低いとインピーダンスが小さく、周波数が高いほどインピーダンスは大きくなる。コイルの単位はヘンリー(H )で、L (H)のコイルのインピーダンスZ(Ω)は、交流の周波数をf(Hz)とすると次の式で計算できる。
Z = 2πfL …(17式)
例えば、5Hのコイルは1kHzの交流に対しては
2 × 3.14 × 1000 × 5 ≒ 31kΩ …(18式)
という値になる。これが10 kHzだったら10倍の310kΩである。
ちなみに、コイルも合成できる。コイルの合成は抵抗のときの規則とまったく同じである。このコイルは、ギターアンプやオーディオアンプの中ではそれほどは出てこない(ちなみにラジオでは必ず出てくる)。コイルの一種であるトランスは定番部品だが、コイルが単独で使われるのは電源回路のチョークコイルぐらいである。電源回路で、交流から直流に変換するとき、交流を通さずに直流を通すコイルの性質を利用するのだ。
トランス
トランスは、下図の左のように、鉄などの磁性体で出来たコアの回りに複数のコイルを巻いた素子である。これで、1次側に交流電圧をかけると、コアに交流の磁力線が発生し、これが2次側に伝わり、2次側のコイルに交流電圧を発生させるのだ。このようにトランスは、交流を伝達する働きをする。2次側のコイルはコアの磁力線の変化に応じた信号が出てくる原理なので、磁力線に変化の無い直流は通さない。
ここで、2次側に出てくる電圧は、1次側のコイルの巻数と2次側のコイルの巻数の比に応じた値になる。たとえば、右の図のように1次側にコイルを100回巻いて、2次側には200回巻いたとすると、巻数比は1:2になり、1次側に100Vの電圧をかけると2次側にはその2倍の200Vの電圧が現れる。このようにトランスは電圧値を変換する性質があるので
変圧器
とも呼ばれていて、電源トランスはこの原理を応用したものである。

|
| トランスの構造と働き |
もうひとつのトランスの重要な働きは
インピーダンス変換
である。いま、下図の左のように巻き数比がn:1のトランスがあり、その2次側に大きさR(Ω)の抵抗を接続したとする。すると、この抵抗値Rはトランスで変換され、1次側から見るとこれがR n
2という値になるのである。例えば、前の例のように巻き数比が2:1のトランスの2次側に100Ωの抵抗をつなぐと、これが1次側からは400Ωに見える、ということになる。ここで、1次と2次というのは便宜的なものなので逆も同じくである。例えば、1次側に400Ωをつなぐと、2次側からは100Ω (= R / n
2)に見える。
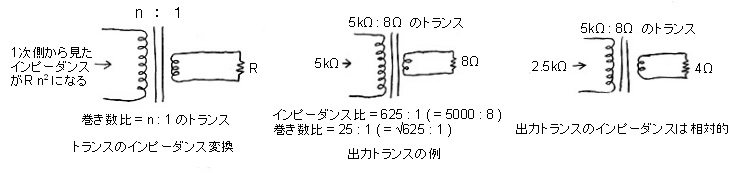
このインピーダンス変換の性質を使ったのが出力トランスである。例えば下図の真ん中のように、5kΩ:8Ωという規格の出力トランスがあるとすると、そのインピーダンス比は
5kΩ : 8Ω = 5000 : 8 = 625 : 1 …(19式)
である。これを巻き数比に直すときは、上の式の左側のルート(平方根)を取れば計算できる。
√625 : 1 = 25 : 1 …(20式)
巻き数比はこのように25:1になっている。巻き数比はとにかく、このトランスはインピーダンスを1/625にする(あるいは、1次側から見ると625倍する)素子なのである。この倍数は相対的なもので、下図の右のように、2次側に4Ωの負荷をつけると1次側のインピーダンスは625倍されて2.5kΩになる。トランスの規格には5kΩ:8Ωと書かれているが、この値以外では使えないというわけではなく、インピーダンスの比が決まっているだけなのだ。とはいえ、何をつないでも625:1になるか、というと現実にはそういうわけではなく、トランスは表示の規格値で性能が出るように設計されているので、その付近で使うのが原則で、あまり外れたインピーダンスをつなぐと思ったように動作しない。ではどれくらい許容されるかであるが、これは使っているトランスにも、用途にもよるので一概に言えないが、ふつう0.5〜2倍ていどならほとんど問題なく使える。
|
| トランスのインピーダンス変換 |
最後に現実のアナログ素子について一言
これまでにお話ししてきたアナログの基礎は、すべて理想的な状態での話である。アナログの世界は、デジタルの世界のように1か0かが確定している世界ではないので、現実には「ゼロ」とか「無限大」とか「通さない」とかいうことはなく、必ず、それぞれ「ゼロではなく微小な量」「無限大ではなくとても大きい値」「ごくわずかは通す」という事態になっている。例えば、コンデンサは直流を通さない、とさっきは言い切ったが、現実のコンデンサという部品の直流抵抗は無限大ではなく、かなり大きいが抵抗値を持っていて、ごくわずかの直流を通す。こういった、本来の働きと異なる性質が、回路に悪さをする場合もあるし、ほとんど影響しないこともある。アナログには「絶対」はない、と考えておいていただきたい。まあ、それだからアナログ回路は面白い、ということにもなるのであろう。















